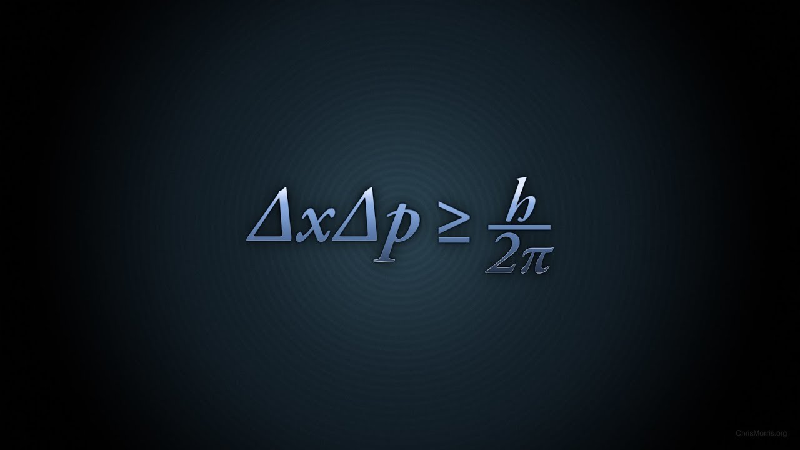In 1927, the German Physicist Werner Heisenberg put forth the famous Heisenberg Uncertainty principle or simply Heisenberg principle which states that ‘the more precisely you know the position of a particle, the less precisely you can simultaneously know the momentum of that same particle. Heisenberg’s Uncertainty principle is one of the keystones of quantum mechanics or quantum physics for a physical world from that of classical physics.
Heisenberg Uncertainty Principle Formula and Relations.
The Heisenberg Uncertainty principle explains certain physical variables like position and momentum. The principle says that it is unable to measure the position(x) and momentum (p) of a particle with absolute precision.
∆x × ∆p ≥ h/4π
∆x = Error in position measurement
∆p = Error in momentum measurement
h= Planck’s constant = 6.626 × 10-34 joule seconds
Since momentum p=mv, then
∆x × ∆mv ≥ h/4π or ∆x × ∆m × ∆v ≥ h/4π
∆v = Error in the measurement of velocity and mass remains constant
∆x × ∆v ≥ h/4πm
This indicates the large uncertainty for the other quantities if the accurate measurement of position and momentum are known.
Applying this to an electron in an atom, m= 9.11 × 10-31Kg
∆x × ∆v ≥ 6.626 × 10-34/4×3.14 × 9.11 × 10-31Kg
∆x × ∆v ≥ 10-4m2s-1
Explanation of the Heisenberg Uncertainty Principle with Example.
If we take an example of an atom, the negatively charged electron orbits a positively charged nucleus. Heisenberg uncertainty principle doesn’t say that they attract each other as they are oppositely charged species because if an electron goes close to the nucleus, the position will be precisely known and error in measuring its momentum will be more. So that the electron will be moving fastly.
Equations of Heisenberg uncertainty principle
There are mainly 2 equations for Heisenberg uncertainty principle,
For position and momentum, the uncertainty principle is:
∆x × ∆p ≥ h/4π
For energy and time, the uncertainty principle is:
∆E × ∆t ≥ h/4π
∆E = Uncertainty in energy and ∆t = Uncertainty in time.
Schrodinger Wave Equation
Schrodinger wave equation (or Schrodinger equation) is developed in 1926 by the Austrian physicist Erwin Schrodinger that describes the dynamics of the quantum mechanical system through wave function in a partial differential equation.
There are two equations; Time-dependent Schrodinger wave equation and Time-independent Schrodinger wave equation.
Time-dependent Schrodinger wave equation is given by,
i= imaginary unit
Ψ = Wave function
Time-independent Schrodinger wave equation is given by,
Physical Significance of the Schrodinger Wave Equation.
An acceptable solution to the Schrodinger wave equation i.e the eigen function or wave function should satisfy the following condition:
- The function should be finite.
- It should be single-valued
- It should be continuous, that means if plotted in space there should not be any break
- Should be continuous
- The function should be normalised,
⌠Ψ2 dt = 1
Summary
- Heisenberg’s Uncertainty principle is one of the keystones of quantum mechanics
- Heisenberg principle which states that ‘the more precisely you know the position of a particle, the less precisely you can simultaneously know the momentum of that same particle.
- For position and momentum, the uncertainty principle is:
∆x × ∆p ≥ h/4π
- For energy and time, the uncertainty principle is:
∆E × ∆t ≥ h/4π
- Schrodinger wave equation describes the dynamics of the quantum mechanical system through wave function in a partial differential equation.